Time to read: 6 min
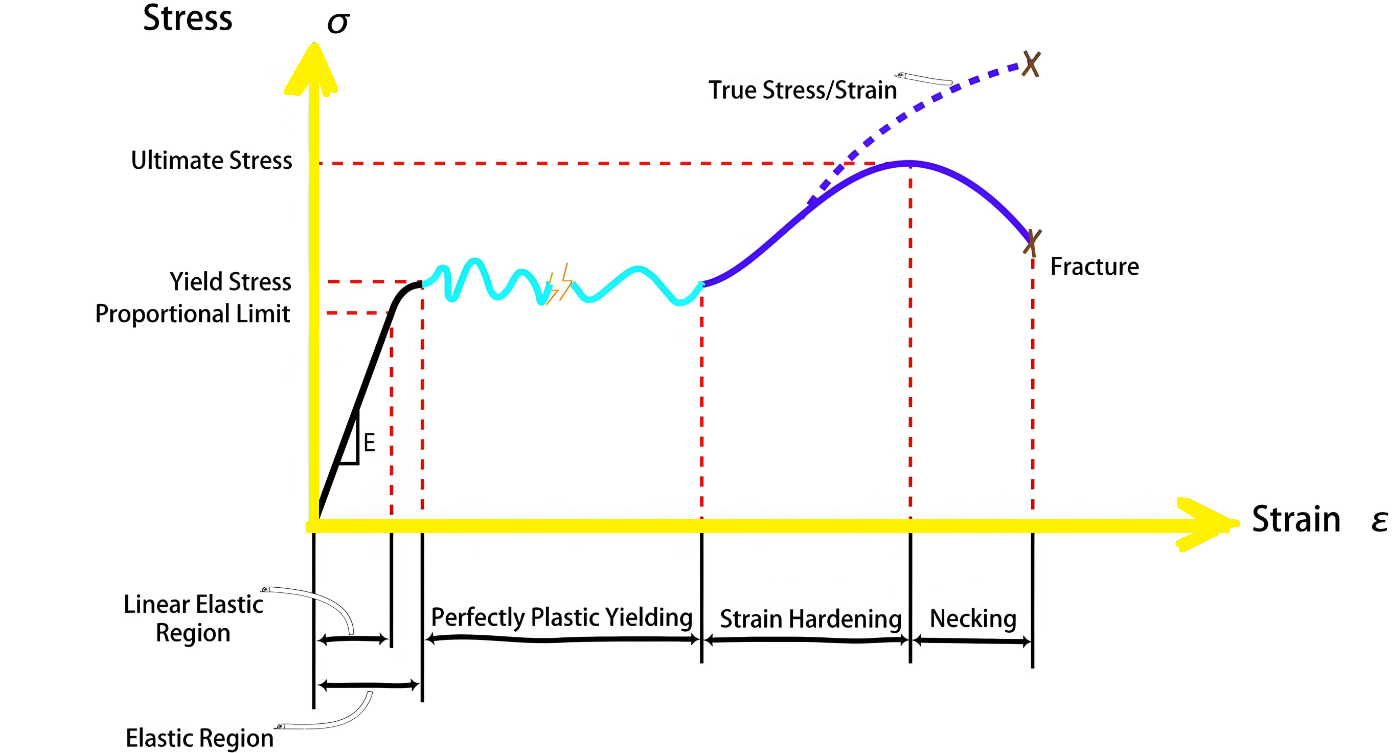
In the realm of material science and engineering, understanding how materials respond to forces is crucial. Two key concepts that describe this behavior are stress and strain. This article will delve into defining stress and strain, their significance, and how they relate to each other.
Define Stress
Stress is a physical quantity that describes the internal resistance of a material to deformation. It is typically caused by an external force applied to a material, and it represents the intensity of that force at a point within the material. Mathematically, stress is defined as the force applied per unit area and is expressed by the formula:
σ=FAσ=AF
where σσ represents stress, FF is the applied force, and AA is the cross-sectional area over which the force is distributed.
Define Strain
Strain, on the other hand, measures the deformation or change in shape of a material in response to an applied force. Unlike stress, strain is a dimensionless quantity that indicates the relative change in size or shape of an object compared to its original state. It is calculated using the formula:
?=ΔLL0?=L0ΔL
where ?? is the strain, ΔLΔL is the change in length of the material, and L0L0 is the original length.
Relationship Between Stress and Strain
The relationship between stress and strain is often described by Hooke's Law, which states that within the elastic limit, the stress applied to a material is directly proportional to the strain produced. This relationship can be expressed as:
σ=E?σ=E?
where EE is the modulus of elasticity or Young's modulus, a material-specific constant that describes its stiffness.
Importance of Understanding Stress and Strain
Understanding stress and strain is vital for various applications:
- Material Selection: Knowing how a material behaves under stress and strain helps engineers select the most suitable material for a given application.
- Design Optimization: Engineers can design components that can withstand specific levels of stress and strain, ensuring safety and reliability.
- Quality Control: By testing materials for their stress-strain behavior, manufacturers can ensure they meet performance standards.
Applications in Various Industries
The principles of stress and strain are applied across various industries:
- Construction: Ensuring the structural integrity of buildings and bridges.
- Automotive: Designing safe and durable vehicles.
- Aerospace: Developing materials for aircraft and spacecraft that can withstand extreme conditions.
Conclusion
Defining and understanding stress and strain are fundamental to material science and engineering. They provide insights into how materials behave under different forces, allowing for the development of safer, more reliable, and efficient designs. At Unofactory, we leverage this knowledge to ensure that the materials we work with meet the highest standards of performance and reliability.




